M203-20251101-Lecture 9-Countability and Probability
- [10:25](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=10:25)
- [11:17](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=11:17.08)
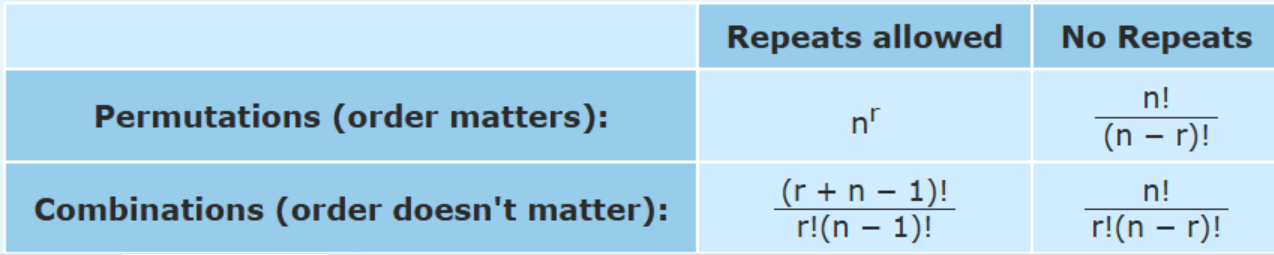
1 ) There are 5 yellow pegs, 4 red pegs, 3 green pegs, 2 blue pegs, and 1 orange peg to be placed on a triangular peg board. In how many ways can the pegs be placed so that no (horizontal) row or (vertical) column contains two pegs of the same color?

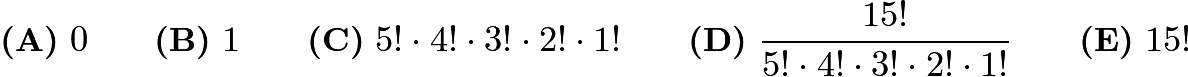
[2000 AMC 10 Problem 13](https://artofproblemsolving.com/wiki/index.php?title=2000_AMC_10_Problems/Problem_13)

Distinguishability matters
Rule of thumb:
- Inanimate objects are usually considered indistinguishable.
- People and living things are considered distinguishable.
- [17:08](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=17:08)
2)
Pat wants to buy four donuts from an ample supply of three types of donuts: glazed, chocolate, and powdered. How many different selections are possible?
(A) 6 (B) 9 (C) 12 (D) 15 (E) 18
[2001 AMC 10 Problem 19](https://artofproblemsolving.com/wiki/index.php?title=2001_AMC_10_Problems/Problem_19)
插板法
|| oo oo
C(n, r) = n! / (r! * (n - r)!)
=6! / (2!(6−2)!)
=6! / 2!×4!
= 15
- [29:52](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=29:52)
4)Pat is to select six cookies from a tray containing only chocolate chip, oatmeal, and peanut butter cookies. There are at least six of each of these three kinds of cookies on the tray. How many different assortments of six cookies can be selected?
(A) 22 (B) 25 (C) 27 (D) 28 (E) 729
[2003 AMC 10A Problem 21](https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_10A_Problems/Problem_21 )
Using the ball and urns/sticks and stones/stars and bars formula
C(n, r) = n! / (r! * (n - r)!)
=8! / (2!(8−2)!)
=8! / 2!×6!
= 28
- [33:29](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=33:29)
8 ) Henry's Hamburger Haven offers its hamburgers with the following condiments: ketchup, mustard, mayonnaise, tomato, lettuce, pickles, cheese, and onions. A customer can choose one, two, or three meat patties and any collection of condiments. How many different kinds of hamburgers can be ordered?
[2004 AMC 10A Problem 12](https://artofproblemsolving.com/wiki/index.php?title=2004_AMC_10A_Problems/Problem_12)
Solution
Think of the condiments as a set with $8$ elements. There are $8$ total condiments to choose from. Therefore, there are $2^8=256$ ways to order the condiments. (You have two choices for each condiment- one choice is to include that condiment, and the other choice is to not include that condiment.) There are also $3$ choices for the meat, making a total of $256 \times 3 = 768$ possible hamburgers.
Subset Problem: Given n objects, what is the number of subsets?
Key - consider from the perspective of each element
- [41:15](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=41:15)
9 ) The $5 \times 5$ grid shown contains a collection of squares with sizes from $1 \times 1$ to $5 \times 5$. How many of these squares contain the black center square?

(A) 12 (B) 15 (C) 17 (D) 18 (E) 20
[2004 AMC 10A Problem 16](https://artofproblemsolving.com/wiki/index.php?title=2004_AMC_10A_Problems/Problem_16))
Since there are five types of squares: $1 \times 1, 2 \times 2, 3 \times 3, 4 \times 4,$ and $5 \times 5$. We must find how many of each square contain the black shaded square in the center.
If we list them, we get that:
- There is $1$ square of size $1 \times 1$ containing the black square
- There are $4$ squares of size $2 \times 2$ containing the black square
- There are $9$ squares of size $3 \times 3$ containing the black square
- There are $4$ squares of size $4 \times 4$ containing the black square
- There is $1$ square of size $5 \times 5$ containing the black square
Thus, the answer is:
$$1 + 4 + 9 + 4 + 1 = 19 \quad \Rightarrow \quad \text{(D) } 19$$

- [45:50](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=45:50)
11) How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?
(A) 41 (B) 42 (C) 43 (D) 44 (E) 45
[2005 AMC 10A Problem 14](https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_10A_Problems/Problem_14)
We are given: "How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?"
Let the number be $x\,y\,z$ with $x \in \{1,\dots,9\}$, $y,z \in \{0,\dots,9\}$.
Condition:
$y = \dfrac{x + z}{2}$
This requires $x+z$ to be even.
---
Case 1: $x$ odd $\Rightarrow$ $z$ odd.
Odd $x$: $1,3,5,7,9$ (5 choices)
Odd $z$: $1,3,5,7,9$ (5 choices)
$\Rightarrow 5 \times 5 = 25$ pairs.
---
Case 2: $x$ even $\Rightarrow$ $z$ even.
Even $x$: $2,4,6,8$ (4 choices)
Even $z$: $0,2,4,6,8$ (5 choices)
$\Rightarrow 4 \times 5 = 20$ pairs.
---
Total $(x,z)$ pairs: $25 + 20 = 45$.
Each pair determines $y = \frac{x+z}{2}$ (always an integer between 0 and 9).
Thus the answer is: $45 \quad \Rightarrow \quad \text{(E) } 45$

- [50:24](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=50:24)
16)How many four-digit positive integers have at least one digit that is a 2 or a 3?
A. 2439
B. 4096
C. 4903
D. 5416
[2006 AMC10A Problem 21](https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_10A_Problems/Problem_21)
# Solution 1 (Complementary Counting)
We want the number of positive 4-digit integers with at least one digit 2 or 3.
Step 1: Total 4-digit integers
- Thousands digit: $1$–$9$ → $9$ choices
- Each of hundreds, tens, units digits: $0$–$9$ → $10$ choices
$\text{Total} = 9 \times 10 \times 10 \times 10 = 9000$
Step 2: Count numbers with NO digit 2 or 3
- Thousands digit: choices are $\{1,4,5,6,7,8,9,0\}$ but can't be $0$ → remove $0,2,3$ from $1$–$9$ leaves $7$ choices
- Each of hundreds, tens, units digits: $\{0,1,4,5,6,7,8,9\}$ → $8$ choices
No 2 or 3=7×8×8×8=3584
Step 3: Subtract $9000 - 3584 = 5416$ $\boxed{E}$
- [56:34](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=56:34)
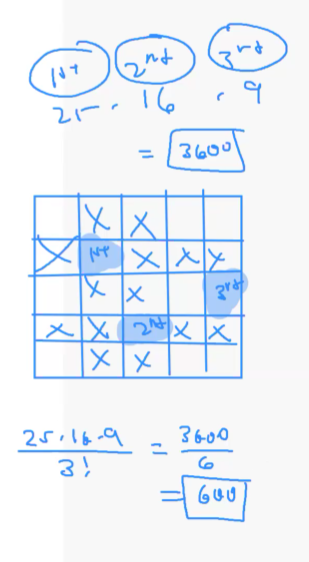
20)A set of $25$ square blocks is arranged into a $5 \times 5$ square. How many different combinations of $3$ blocks can be selected from that set so that no two are in the same row or column?
(A) $100$
(B) $125$
(C) $600$
(D) $2300$
(E) $3600$
[2007 AMC10B Problem 20](https://artofproblemsolving.com/wiki/index.php?title=2007_AMC_10B_Problems/Problem_20)
- [1:01:54](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=1:01:54.19)
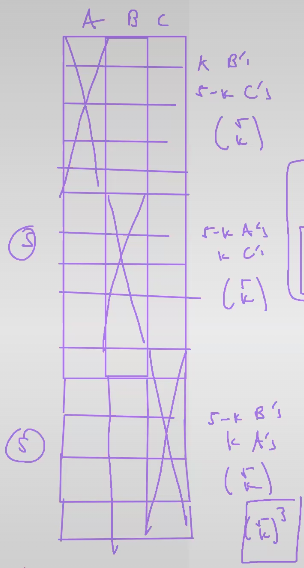
25)How many 15-letter arrangements of 5 A's, 5 B's, and 5 C's have no A's in the first 5 letters, no B's in the next 5 letters, and no C's in the last 5 letters?
A. $\displaystyle \sum_{k=0}^{5} \binom{5}{k}^3$
B. $\large 3^5 \cdot 2^5$
C. $\large 2^{15}$
D. $\dfrac{15!}{(5!)^3}$
E. $\large 3^{15}$
[2003 AMC12A Problem 20](https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12A_Problems/Problem_20)
2. Compound Events and Combination
概率论是计数的延伸,它量化了事件发生可能性的大小。
| | |
| --------- | ------------------------------------- |
| 概念 | 定义与公式 |
| 基本定义 | `P(事件) = 目标结果数 / 所有可能结果总数` |
| 事件的并集 | `P(A 或 B) = P(A) + P(B) - P(A 与 B)` |
| 补集事件 | `P(A) = 1 - P(非A)` |
| 独立事件 | 若A和B相互独立,则 `P(A and B) = P(A) * P(B)` |
问题重构与对称性:视角的转变
对于某些涉及序贯过程的概率问题,与其使用复杂的概率树,不如重新构想问题,利用对称性来简化。
- [1:21:00](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=1:21:00)
A box contains exactly five chips, three red and two white. Chips are randomly removed one at a time without replacement until all the red chips are drawn or all the white chips are drawn. What is the probability that the last chip drawn is white?
2001 AMC 12 Problem 11
Solution:
Think of continuing the drawing until all five chips are removed form the box. There are ten possible orderings of the colors: RRRWWRRRWW, RRWRWRRWRW, RWRRWRWRRW, WRRRWWRRRW, RRWWRRRWWR, RWRWRRWRWR, WRRWRWRRWR, RWWRRRWWRR, WRWRRWRWRR, and WWRRRWWRRR. The six orderings that end in RR represent drawings that would have ended when the second white chip was drawn.
Imagine drawing until only one chip remains. If the remaining chip is red, then that draw would have ended when the second white chip was removed. The last chip will be red with probability $\dfrac{3}{5}$.
二项分布用于计算在一系列固定的、独立的、只有两种结果(成功/失败)的试验中,获得特定成功次数的概率。
• 适用场景:`n` 次重复独立试验,每次成功的概率为 `p`。
• 公式:在 `n` 次试验中,恰好成功 `r` 次的概率为: `P(r) = C(n, r) * pʳ * (1-p)ⁿ⁻ʳ`
◦ `C(n, r)`:在 `n` 次试验中选择 `r` 次成功的方式数。
◦ `pʳ`:`r` 次成功的概率。
◦ `(1-p)ⁿ⁻ʳ`:`n-r` 次失败的概率。

- [1:28:30](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=1:28:30)
3)Coin A is flipped three times and coin B is flipped four times. What is the probability that the number of heads obtained from flipping the two fair coins is the same?
2004 AMC 10A Problem 10
[[media/16d3685140934e8bc273be0b9b202b55_MD5.png|Open: Pasted image 20251120184547.png]]

- [1:35:26](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=1:35:26)
4 ) Two eight-sided dice each have faces numbered 1 through 8. When the dice are rolled, each face has an equal probability of appearing on the top. What is the probability that the product of the two top numbers is greater than their sum?
2004 AMC 10B Problem 11

- [1:39:53](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=1:39:53)
-
11 )
For a particular peculiar pair of dice, the probabilities of rolling 1,2,3,4,5 and 6 on each die are in the ratio 1:2:3:4:5:6. What is the probability of rolling a total of 7 on the two dice?
[2006 AMC 10B Problem 21](https://artofproblemsolving.com/wiki/index.php?title=2006_AMC_10B_Problems/Problem_21)
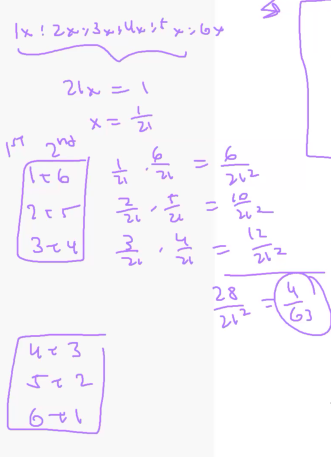
- [1:57:30](file:///C:/Users/mg_ku/Downloads/M203-20251101-Lecture%209-Countability%20and%20Probability.mp4#t=1:57:30)
14 ) The faces of a cubical die are marked with the numbers $1$, $2$, $2$, $3$, $3$, and $4$. The faces of another die are marked with the numbers $1$, $3$, $4$, $5$, $6$, and $8$. What is the probability that the sum of the top two numbers will be $5$, $7$, or $9$?
$\mathrm{(A)}\ 5/18\qquad\mathrm{(B)}\ 7/18\qquad\mathrm{(C)}\ 11/18\qquad\mathrm{(D)}\ 3/4\qquad\mathrm{(E)}\ 8/9$
[2008 AMC 10B Problem 20](https://artofproblemsolving.com/wiki/index.php/2008_AMC_10B_Problems/Problem_20?srsltid=AfmBOoo8ufE6J60rJI6BRy9Rw_zqlTU3wukdxnftokFhXtBsWXV20ru0)
[[media/2a4f2c0ad4839af93ba62610c06ad4c0_MD5.png|Open: Pasted image 20251121121434.png]]
